
Wondering how many tulip bulbs per square foot you should plant? Calculating the right number is essential for achieving a vibrant and full garden display, and it’s easier than you might think with just two simple steps.
- Determine the square footage of the area you are planting. See the formulas provided below.
- Determine the number of bulbs to plant per square foot (the density). We provide a recommended planting density for every item on this website, along with a calculator that will do the math for you.
If you have any questions about calculating square footage or how many bulbs to plant per square foot, don’t hesitate to reach out or give us a call.
Please note: Planting bulbs is hard work. Landscape professionals and experienced gardeners can dive right in and order as needed. However, for those new to planting bulbs, we recommend starting small to get a feel for the process. Once you see the results in spring and feel confident you can handle more, you can increase your order the following fall. This gradual approach is kinder to your back, your budget, and your learning curve.
Rectangle and Square
The area of a rectangle and a square is found by multiplying the length (L) by the width (W).

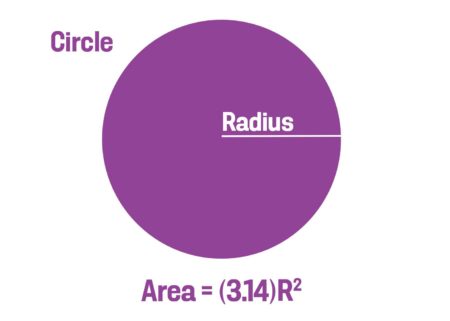
Circle
The area of a circle is the radius squared (i.e., the radius multiplied by itself) multiplied by pi (~3.14). And the radius is equal to one-half the diameter of the circle.
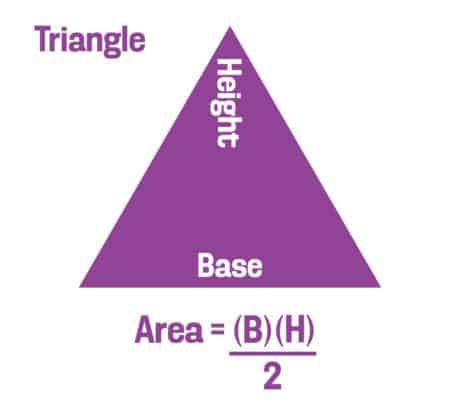
Triangle
The area of a triangle is one-half the base (B) multiplied by the height (H).
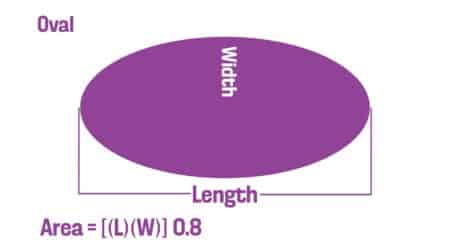
Oval
The area of an oval is the length (L) multiplied by the width (W), multiplied by 0.8.
Irregular Shapes
To find the area of a large irregular shape, divide it into a series of smaller units equally spaced along a measured line. This method will calculate the area to within 5 percent.
- Determine the axis line. This is the longest axis of the shape, shown below as A to B.
- Mark several perpendicular lines along the axis line to divide it into several segments of equal depth. To ensure accuracy, use as many lines as possible. The more irregular the shape, the more lines you will need.
- Measure the width of the bed at each perpendicular line.
- Calculate the area by adding the lengths of all the perpendicular lines and multiplying by the distance between the lines.
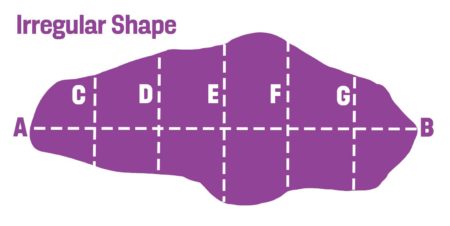
Let’s Look at an Example
To calculate how many tulip bulbs per square foot to plant in this area, start by determining the layout. The distance between points A and B is 60 feet, divided into six equal-depth segments of 10 feet by five perpendicular lines. The perpendicular lines have the following measurements:
C = 19 feet
D = 22 feet
E = 23 feet
F = 19 feet
G = 13 feet
The approximate area is: (19 + 22 + 23 + 19 + 13) x 10 = 960 sq. ft.


